Hier folgen einige Aufgaben des schulinternen Wettbewerbs:

Probleme beim Schulfest

Bei einem Schulfest sollen alle Schüler der Schule geordnet auf den Sportplatz laufen.

Der Sportlehrer stellt fest, daß ein Schüler übrig bleibt, wenn er in Zweierreihen antreten läßt.Auch beim Aufstellen in Dreierrreihen bleibt einer übrig.

Sogar bei Vierer-, Fünfer- und Sechserreihen-Aufstellung bleibt jeweils ein Schüler übrig. Erst bei Aufstellung in Siebener- Reihen bleibt keiner übrig.

Wieviel Schüler hat die Schule mindestens?

(entnommen aus: Hahn/Dzewas: Mathematik 6, S. 60)

---

1. Problem des Monats

1. für die Klasse 5

Ein Mathematiklehrbuch umfaßt 196 Seiten. Die Seitenzahlen für die ersten beiden Seiten und für die letzte Seite wurden nicht gedruckt, d. h. die Numerierung beginnt mit 3.

a) Wie viele Ziffern wurden zum Numerieren der übrigen Seiten verwendet?

b) Wie oft wurde dabei die Ziffer 0 gedruckt?

c) Das dickere Geschichtsbuch, dessen Numerierung auch mit der Ziffer 3 beginnt, hat insgesamt 910 Ziffern für die Seitenzahlen. Welche Seitenzahl steht auf der letzten Seite?

2. für die Klassen 6 und 7

Frau Knobel ist Mathematiklehrerin. Eines Tages klingelt bei ihr ein junger Mann und versucht, sie zum Abonnieren einer Zeitschrift zu überreden. Frau Knobel lehnt zuerst ab, wird dann aber freundlicher, als sie hört, daß der junge Mann Mathematikstudent ist. Sie sagt:" Wenn Sie herausbekommen. wie alt meine Töchter sind, werde ich ihre Zeitschrift für ein Jahr bestellen. Also passen Sie auf: Wenn ich die Alter meiner 3 Töchter miteinander multipliziere, erhalte ich 36."

Der Student überlegt und sagt dann: "Das reicht nicht aus, um das Problem zu lösen!"

"Richtig", sagt Frau Knobel."Wenn ich aber das Alter meiner Töchter addiere, so ergibt sich unsere Hausnummer!".

Der junge Mann rennt rasch vor das Haus, kommt zurück und und sagt:"Sie wollen mich wohl auf den Arm nehmen. So ist die Aufgabe immer noch nicht lösbar." Darauf Frau Knobel: "ja, aber meine älteste Tochter spielt Geige."

"Na, das reicht,"sagt der Mathematikstudent und nennt richtig das Alter der Töchter.

Wie alt sind sie?

 

3. für die Klassen 8 und 9

Es sind alle natürlichen Zahlen n anzugeben, für die die Zahl

z = (n + 17) / (n -3) ebenfalls eine natürliche Zahl ist.

a) Erstelle eine Tabelle, in der du n und das jeweilige z einträgst.

b) Erkennst Du zwischen den Zahlen der Tabelle einen Zusammenhang? Erkläre.

---

2. Problem des Monats

 Eine kleine Lokalbahngesellschaft in einer verschlafenen Gegend geht aufgrund des schlechten Wirtschaftens in Konkurs und wird von der Deutschen Bahn A.G. übernommen In diesem Zusammenhang geht auch das historische Bahnhofsgebäude von Hintertupfingen in Bahnbesitz über. Der Stadtrat von Hintertupfingen will nun genau dieses Gebäude aufgrund seines historischen Wertes erhalten. Kurzerhand schreibt er der Deutschen Bahn und überredet sie zu der Zusage es auch weiterhin zu nutzen.

Als ein Vertreter der Deutschen Bahn A.G. zu einer Inspektion kommt , stellt er fest ,daß eigentlich nur die Karten der Zuganzeigetafel erneuert werden müssen. Sie werden von der Frau des Bahnhofsvorstehers an jedem Morgen in die Tafel gesteckt, um die Nummern der abfahrenden Züge anzuzeigen:

 

An einem bestimmten Tag sieht die Tafel z. B. so aus:

Zug 1	1	8	5
Zug 2	5	3	4
Zug 3	7	8	3
Zug 4	7	5	3
Zug 5	9	1	2

 

Doch als ein Restaurator sagt ,daß je Restaurierung einer Karte (Vorder- und Rückseite) 100 DM zu bezahlen sind, erleidet der Bahnvertreter fast einen Schock. Er rechnet:

5 Zeilen x 3 Plätze je Zeile	=	150 Plätze
150 Ziffern x 100 DM jeZiffer	=	150 Ziffern
150 Ziffern x 100 DM je Ziffer	=	15 000 DM

So viel Geld steht gar nicht zur Verfügung ; durch die Umstellung der Bundesbahn in eine A.G. ist das Geld knapp geworden.

Als er sein Problem später einem Kollegen vorträgt, meint dieser:   "In deiner Rechnung berücksichtigst du mehreren Faktoren nicht. Es können alle Züge von Zug 000 bis Zug 999 angezeigt werden ,ohne 150 Karten zu restaurieren. Einige Karten müssen zwar erneuert werden, aber längst nicht alle. Nicht alle fünf Züge können dieselbe Schnapszahl als Zugnummer haben ,wodurch es nicht vorkommen kann, daß eine Ziffer auch fürfzehn mal benötigt wird. Verwendet man eine Karte mit der Aufschrift 6 auf dem Kopf ,so steht dort 9. Und zuletzt kann doch auf der Rückseite jeder Karte auch eine Nummer stehen".

Aufgaben:

a) Wie viele Karten müssen insgesamt erneuert werden?

Wie hoch sind die tatsächlich entstehenden Kosten?

b) In einem anderen Bahnhof mit dem selben Problem fahren jeden Tag nur 3 Züge ab. Sie tragen jedoch fünfstellige Nummern.

Wie viele Karten werden mindestens benötigt?

c1) Bei einem Neukauf solcher Karten nach historischem Vorbild würden die ersten 25 Karten 125,- DM pro Stück, die nächsten 25 Karten 30 DM weniger (pro Stück) kosten und dann nur noch 60 DM pro Karte kosten. Ab 100 Karten kostet jede nur noch 45 DM.

Welche Lösung (Neukauf oder Restaurierung) wär, in den Fällen a) und b) zu empfehlen?

c2) Bei einem Neukauf hangefertiger Karten nach historischen Vorbild würde die erste Karte 200 kosten, jede weitere Karte 2,50 DM weniger. Welche Lösung (Neukauf oder Restaurierung) wäre hier bei gleichen Restaurierungskosten zu empfehlen? Was wäre, wenn jede folgende Karte 3,25 DM billiger wäre als ihre Vorgängerin?

(Diese Aufgabe stammt von Uwe Stegemann, Klasse 12 , Beisenkamp Gymnasium, Hamm).

---

3. Problem des Monats

1. Für die Klasse 5:

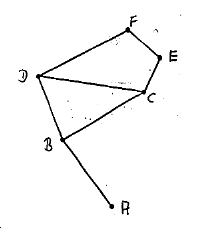
Zwischen den Städten A, B, C, D, E und F gibt es ein Autobahnnetz. Der Plan zeigt die bestehenden Verbindungen an. 1 cm in dieser Zeichnung entspricht 20 km in Wirklichkeit.

a) gesucht ist die jeweils kürzeste Autobahnverbindung von einer Stadt zu den übrigen. Versuche, die Entfernungen übersichtlich in einer Tabelle darzustellen.

b) Weiterhin sind auch die Entfernungen per Luftlinie zwischen den einzelnen Städten gesucht. Erläutere, wie du sie findest.Kann man berechnen, wie viele solcher Luftlinien-Entfernungen es hier gibt?Wie?

c) Welche Städte liegen im Umkreis  von 100 km von der Stadt B?  

Hinweis: Die Strecke AB ist 3.1 cm lang.

 

2. Für die Klassen 6 und 7:

1. Ein Rätsel aus dem Rechenbuch des Adam Riese (1574):

Ein Sohn will von seinem Vater dessen Alter wissen. Er antwortet: 
"Zähle zusammen das Doppelte meines gegenwärtigen Alters und die Hälfte
davon. Dann addiere nochmals ein Viertel meines Alters hinzu. Fügst Du 
nun noch ein Jahr hinzu, so erhälst Du 100 Jahre."
 

Wie alt war der Vater?

2. J. Chrst. Schäfer (19. Jahrhundert)

Ein junger Hirte ließ mit Freuden
1008 Schafe weiden
Bis der Sonne letzter Strahl
Entwich aus seinem grünen Thal,
Und grauer Abend war geworden.
jetzt führte er sie in 12 Horden,
Doch so als jegliche 2 mehr
Enthielt als das nächstvor'ge Heer.
Sag, wieviel in die erst kommen,
und aus jede andre ausgenommen?
 

(aus: Wunder der Rechenkunst, 1857)

Wieviele Schafe hatte die 1., 2, 3..... Herde? Erkläre!

 

3. für die Klassen 8 und 9:

Ersetze das Fragezeichen!

Läßt sich die Lösung auch auch durch Gleichungen berechnen? Erkläre!

zurück

zurück zur Homepage

learn:line- Mediothek

© Monika Schwarze:  7/99